Kümeler Konusu

Kümeler

Kümenin kesin bir tanımı yoktur. Matematikte küme tanımsız bir kavram olmakla beraber, küme denince aklımıza  nesnelerden meydana gelen topluluk gelir.

Küme kavramını örneklerle açıklayalım.

Örnek:

A = { 1, 3, a, 4} bir kümedir. 1, 3, a, 4 bu kümenin elemanlarıdır. A kümesinin 4 tane elemanı vardır. Bunu s(A) = 4 şeklinde yazarak belirtiriz. Bir elemanın kümeye ait olduğunu ∈, ait olmadığını ∉ işaretiyle belirtiriz.

1∈ A, 3 ∈ A, a ∈ A, 4 ∈ A, 5 ∉A dır.

Örnek:

A = { #, 2, {1, 3}, 4} kümesi 4 elemanlıdır.

Yani s(A) = 4 tür.

 # ∈ A, 2 ∈ A, {1, 3} ∈ A, 4 ∈ A dır. Ancak  1 ∉ A ve 3 ∉ A dır.

Liste Yöntemi

Kümenin bütün elemanlarını { } sembolü içerisine yazarak belirttiğimiz kümeye liste yöntemi ile gösterim diyoruz.

Örnek:

A = { 3, 6, 7, 8, 12}

B = { a, x, y, z, t, k}

C = { Mehmet, Hasan, Mustafa, Kemal, Osman, Ali, Zeynep, Gonca}

D = { keçi, koyun, tavuk, inek, at, zebra}

kümeleri liste yöntemi ile gösterilmiştir.

Ortak Özelik Yöntemi

Kümelerin elemanlarının ortak özelliğini belirterek yazdığımız kümeye ortak özellik yöntemi ile yazılmış küme denir.

Örnek:

A = { x | x, haftanın günleri}

B = { x | x, sınıfımızdaki gözlüklü erkek öğrenciler}

C = { x | -3 < x <20, x tek sayı }

kümeleri ortak özelik yöntemi kullanılarak yazılmış kümelerdir.

Boş Küme

Hiç elemanı olmayan kümeye boş küme denir. Boş küme { } veya ∅ simgesi ile gösterilir.

s(A) = 0 dır. Yani boş kümenin eleman sayısı sıfırdır.

Örnek:

A = {0} kümesi boş küme değildir.

0 ∈ A dır ve s(A) = 1 dir.

B = {∅} kümesi boş küme değildir. ∅ ∈ B dir. s(B) = 1 dir.

C = { x | x2 + 4 = 0, x reel sayı} kümesi boş kümedir.

Çünkü x2 + 4 = 0 ⇒ x2 = -4 olur. Karesi sıfırdan küçük bir sayıya eşit olan bir reel sayıl olmadığı için C kümesi boş kümedir.

C = ∅ dir. s(C) = 0 dır.

Eşit Kümeler

 Aynı elemanlardan oluşan kümelere eşit kümeler denir.

Örnek:

A = { x : 2 < x < 8, x asal sayı }

B = { x : 2 ≤ x < 9, x tek sayı }

kümelerini karşılaştıralım.

A = { 3, 5, 7 } ve

B = { 3, 5, 7 } olur.

A ve B kümlerinin bütün elemanları aynı olduğundan A = B ve s(A) = s(B) dir.

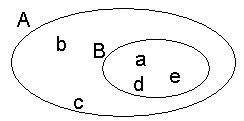
Venn Şeması

Kümenin elemanlarını kapalı eğrilerle çevrilmiş düzlem parçaları ile belirtmeye, kümenin venn şeması ile gösterilişi denir.

Örnek:

A = { a, b, c, d }

B = { Mehmet, Cihat, Süleyman }

kümeleri Venn şeması ile 

şeklinde gösterilir.

Alt Küme

 Bir B kümesinin bütün elemanları bir A kümesinin de elemanları ise B kümesi A kümesinin alt kümesidir denir. B ⊂ A şeklinde yada A ⊃ B şeklinde gösterilir, A kapsar B diye okunur.

Örnek:

A = { a, b, c, d, e}  ve

B = { a, d, e } ise

A kümesi B kümesini kapsar. Yani B kümesi A kümesinin alt kümesidir.

B ⊂ A veya A ⊃ B şeklinde gösterilir.

Bunun venn şeması ile gösterimi

şeklindedir.

Örnek:

A = { 1, 2, 3, 4, 5}

B = { 1, 3, 5, 7} ise B kümesinin 1, 3, 5 elemanları A kümesinin de elemanıdır. Ancak elemanlarından 7 A kümesinin elemanı değildir. O halde A kümesi B kümesini kapsamaz.

Alt Küme Özellikleri:

1. ∅ = { } = boş küme, her kümenin alt kümesidir
2. Her küme kendisinin alt kümesidir. A ⊃ A, B ⊃ B, ∅ ⊃ ∅ gibi
3. İki kümeden her biri diğerinin alt kümesi ise bu iki küme eşittir. A ⊃ B ve B ⊃ A ise A = B dir.
4. A ⊃ B ve B ⊃ C  ise A ⊃ C dir.

Alt küme sayısı:

Bir kümenin eleman sayısı: n ise

Alt küme sayısı: 2n

Öz alt küme sayısı: 2n - 1 tanedir.

Örnek:

A = { 1, a, {2, 3}, 4, #, b} kümesinin

eleman sayısı: s(A) = 6

alt küme sayısı: 26 = 64

öz alt küme sayısı: 26 - 1 = 63 dür.

Uyarı:

n ve r doğal sayı ve n ≥ r ise

C( n, r ) = n! / (n - r)!. r! dir.

Bu bilgiyi n elemanlı bir kümenin r elemanlı alt kümelerinin sayısını bulurken kullanacağız.

Örnek:

A = {a, b, c, d, e} kümesinin 2 elemanlı alt kümelerinin sayısı kaçtır?

s(A) = 5 tir.

C(5, 2) = 5! / (5 - 2)!. 2!

= 120 / 12

= 10 dur.

Örnek:

32 tane alt kümesi bulunan bir A kümesinin en fazla 2 elemanlı alt kümelerinin sayısı kaçtır?

Çözüm:

n elemanlı bir kümenin alt kümelerinin sayısı: 2n dir.

2n = 64 ise

2n = 26 ise n = 6 dır.

Bizden istenen alt kümeler: 0 elemanlı, 1 elemanlı ve 2 elemanlıdır.

0 elemanlı alt küme satısı: 1( boş küme)

1 elemanlı alt küme sayısı: 5(eleman sayısı kadar)

2 elemanlı alt küme sayısı: C(5, 2) = 5! / (5 - 2)!. 2! = 5.4.3.2.1 / 3.2.1.2.1 = 10 dur.

1 + 5 + 10 = 16

Kümelerin Birleşimi

A ve B kümelerinin ortak elemanlarından birer tane (ortak eleman varsa) ortak olmayan elemanların tamamı alınarak oluşturulan yeni kümeye A ve B kümelerinin birleşimi denir.

A U B = { x ∈ A veya x ∈ B} biçiminde yazılır.

A U B kümesi venn şeması ile

şeklinde gösterilir. Taralı bölgenin tamamı A U B kümesidir.

Birleşimin Özellikleri

1. A U A = A dır.
2. A U ∅ = ∅ U A = A dır.
3. A U B = B U A (Değişme)
4. (A U B) U C = A U (B U C) = A U B U C (Birleşme)
5. A ⊂ A U B, B ⊂ A U B

Kümelerin Kesişimi (Ara Kesit)

A ve B kümeleri verilsin. A ve B kümelerinin ortak elemanlarını alarak oluşturulan yeni kümeye A kesişim B kümesi denir.

 A ∩ B = { x | x ∈ A ve x ∈ B } biçiminde yazılır.

 C ∩ D = ∅ ise C ve D kümelerinin ortak elemanı yoktur. Ortak elemanı olmayan kümelere ayrık kümeler denir.

Kesişim kümesi ile ayrık kümeler venn şeması ile

biçiminde gösterilir.

 Örnek:

A = {-3, -2, -1, 0, 1, 2, 3} ve

B = { x | 2x -5 < 7, x doğal sayı} ise A ∩ B kümesini bulalım.

B = {0, 1, 2, 3, 4, 5}

A ∩ B = {0, 1, 2, 3} bulunur.

Venn şeması ile

 biçiminde gösterilir.

Kesişimin Özellikleri

1.  A ∩ A = A
2. A ∩ ∅ = ∅ ∩ A = ∅ dır.
3. A ∩ B = B ∩ A (Değişme)
4. (A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C (Birleşme)
5. A ∩ B ⊂ A, A ∩ B ⊂ B

Kümelerin kesişim ve birleşimi ile ilgili bağıntılar:

1. A U (B ∩ C) = (A U B) ∩ (A U C)
2. A ∩ (B U C) = (A ∩ B) U (A ∩ C)
3. s(A U B) = s(A) + s(B) - s(A ∩ B)
4. s(A U B U C) = s(A) + s(B) s(C) - s(A ∩ B) - s(A ∩ C) - s(B ∩ C) + s(A ∩ B ∩ C)

Tümleme

Bir kümenin tümleyeninden söz edebilmek için ilk önce evrensel küme adı verilen ve yeteri kadar elemanı olan bir küme belirlemeliyiz.

Evrensel kümeyi: E, A kümesinin tümleyenini de A' biçiminde göstereceğiz.

A' = { x | x ∉ A ve x ∈ E} biçiminde tanımlanır.

Venn şeması ile

şeklinde gösterilir

Tümlemenin Özellikleri

1. (A')' = A
2. (A U B)' = A ' ∩ B'
3. (A ∩ B)' = A' U B'
4. A ⊂ B ⇔ B' ⊂ A'
5. ∅' = E, E' = ∅
6. A U A' = E
7. A ∩ A' = ∅
8. s(A) + s(A') = s(E)

İki Küme Farkı

Aynı E evrensel kümesinde A, B kümeleri verilsin, A ya ait olup da B ye ait olmayan elemanlardan oluşan kümeye A ile B nin farkı denir ve A / B veya A - B şeklinde yazılır.

A - B = A / B = { x | x ∈ A ve x ∉ B } biçiminde ifade edilir.

x ∉ B ⇒ x ∈ B' dir. O halde;

A - B = { x | x ∈ A ve x ∈ B' } = A ∩ B' olur

Venn şeması ile

şeklinde gösterilir.

Sıralı İkili

Sıralı İkili

a ve b gibi herhangi iki nesneden birinin diğerinden önce (örneğin a'nın) gelmesi önemli ise, bu durum (a, b) şeklinde gösterilir. Buna sıralı ikili denir. Sıralı ikililerde sıra önemlidir.

(a, b) ≠ (b, a) olduğu halde

{a, b} = {b, a} dır.

Bileşenleri aynı olan ikililere özdeş ikililer denir.

Yani : (a, b) = (c, d) ise

a = c, b = d dir.

(a, b) ikilisinde a'ya birinci bileşen b'ye ikinci bileşen denir.

Kartezyen Çarpım

A ve B gibi herhangi iki kümeden, birinci bileşeni A'dan ikinci bileşeni B'den alınmak, suretiyle oluşturulan sıralı ikililerin tümünün kümesine A ile B nin kartezyen çarpımı denir ve A x B biçiminde gösterilir. Kısaca,

A x B = {(x, y) : x ∈ A ve y ∈ B} dir.

Uyarı:

Kartezyen çarpımının her elemanı bir sıralı ikili ve sıralı ikililerde sıra önemli olduğuna göre;

A x B ≠ B x A dır. Yani kartezyen çarpımda değişme özelliği yoktur.

Kartezyen Çarpımın Eleman Sayısı

A ve B kümelerinin eleman sayıları, s(A) = m ve s(B) = n ise;

s(A x B) = s(A).s(B) = m.n dir.

Uyarı:

s(A x B) = s(B x A) olduğunu unutmayınız.

Kartezyen Çarpımın Şeması

A = {a, b, c} ve B = {3, 4} ise

A x B = {(a,3), (a, 4), (b, 3), (b, 4), (c, 3), (c, 4)} kartezyen çarpımının şeması aşağıdaki gibidir. 

Kartezyen Çarpımının Grafiği

A = {1, 2} ve B = {1, 2, 3} ise;

A x B yazılışında A'nın elemanları yatay (apsis) eksende, B'nin elemanları düşey (ordinat) eksende, B x A yazılışında ise B'nin elemanları yatay (apsis) eksende, A'nın elemanları düşey (ordinat) eksende işaretlenir.

Kısaca; İlk harfe ait elemanlar yatay (apsis), ikinci harfe ait elemanları da düşey (ordinat) eksende gösterilir.

Kartezyen Çarpımın Özellikleri

• A x B ≠ B x A (Kartezyen çarpımda değişme özelliği yoktur.)
• A x (B x C) = (A x B) x C (Birleşme özelliği vardır.)
• A x (B U C) = (A x B) U (A x C) 
• A x (B ∩ C) = (A x B) ∩ (A x C) (Dağılma özelliği vardır.)

A ve B kümeleri verildiğinde;

1. Her iki kümenin elemanları da sayılamayan (sonsuz) çoklukta ise A x B ve B x A nın grafiği bir alan oluşturur.
2. A'nın elemanları sayılamaz, B'nin elemanları sayılabilir çoklukta ise A x B nin grafiği x-eksenine paralel doğrular,
3. A'nın elemanları sayılabilir, B'nin elemanları sayılamaz çoklukta ise A x B nin grafiği y-eksenine paralel doğrular oluşturur.

Bağıntı

A ve B herhangi iki küme olmak üzere A x B kartezyen çarpımı kümesinin β gibi herhangi bir alt kümesine, A dan B ye bağıntı denir.

A = {a, b}, B = {1, 2, 3} kümeleri için;

A x B = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b,3)} kartezyen çarpımının her alt kümesi, A dan B ye bir bağıntıdır. Bu bağıntıların bazıları aşağıda gösterilmiştir.

β1 = {(a, 1), (a, 2), (a, 3)}

β2 = {(b, 1)}

β3 = {(a, 1), (a, 2), (a, 3), (a, 4)}

β4 = {(a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)}

β4 bağıntısından da anlaşılabileceği gibi A x B kümesinin kendisi de aynı zamanda bir bağıntıdır.

A x B kümesi 6 elemanlı olduğundan A x B nin 26 = 64 tane alt kümesi vardır. Bu 64 tane kümenin her biri A'dan B'ye bağıntıdır.

s(A) = m, s(B) = n ise A'dan B'ye yada B'den A'ya yazılabilecek tüm bağıntıların sayısı 2m.n tanedir.

Kartezyen çarpımın değişme özelliği olmadığından bir bağıntının belirtilebilmesi için, o bağıntının kuralının bilinmesi gereklidir. Yani A'dan B'ye mi yoksa B'den A'ya mı olduğu bilinmelidir.

Bir Bağıntının Tersi

A'dan B'ye tanımlanan bir β bağıntısındaki ikilileri yer değiştirerek B'den A'ya yeni bir bağıntı elde edebiliriz. Elde edilen bu yeni bağıntıya β'nin ters bağıntısı denir ve β-1 ile gösterilir. Kısaca;

β = {(x, y) : x  ∈ A, y  ∈ B}

β-1 = {(y, x) : x  ∈ A, y  ∈ B}

Bağıntının Özellikleri

Bir kümede tanımlı bağınıtının aşağıdaki özellikleri vardır.

I. Yansıma Özelliği

β, A'da tanımlı bir bağıntı olsun.

"x ∈ A için (x, x) ∈ β ise β bağıntısının yansıma özelliği vardır denir. Ya da β yansıyan bağıntıdır denir. 

n elemanlı bir A kümesi verilmiş olsun.

m = n2 ise

• A da tanımlı tüm yansıyan bağıntıların sayısı 2 m-n tane olur.
• β yansıyan bir bağıntı ise β nin kartezyen diyagramında y = x üzerinde n tane nokta vardır. 

II. Simetri

β, A'da tanımlı bir bağıntı olsun.

"(x, y) ∈ β iken (y, x) ∈ β ise β simetriktir ya da β bağıntısında simetri özelliği vardır denir. 

• β simetrik bağıntı ise β = β-1 dir.
• n elemanlı bir A kümesinde tanımlanabilecek simetrik bağıntıların sayısı 2n.(n+1)/2 tanedir.
• n elemanlı  bir A kümesinde tanımlanabilecek yansıyan ve simetrik bağıntıların sayısı 2(n²-n)/2 tanedir.

 III. Ters - Simetri

β, A'da tanımlı bir bağıntı olsun.

• x ≠ y için "(x, y) ∈ β iken (y, x) ∉ β ise veya
• "(x, y) ∈ β ve (y, x) ∈ β iken x = y oluyorsa, β bağıntısı ters-simetriktir. 

Uyarı:

1. Ters-simetrik olmayan bir bağıntının simetrik, simetrik olmayan bir bağıntının ters-simetrik olması gerekmez
2. Ters-simetrik bir bağıntıda bileşenleri aynı olan ikililerin bulunması, ters simetriğe aykırı değildir.
3. Ters-simetrik bir bağıntının grafiğinde y = x doğrusuna göre simetrik eleman yoktur.

IV. Geçişme

 β, A'da tanımlı bir bağıntı olsun.

(x, y) ∈ β ve (y, x) ∈ β iken (x, z) ∈ β oluyorsa, β geçişken bir bağıntıdır ya da β bağıntısında geçişme özelliği vardır.

Özel Bağıntılar

Denklik Bağıntısı

A'da tanımlı bir bağıntının 

1. Yansıma
2. Simetri
3. Geçişme

özellikleri varsa bu bağıntıya denklik bağıntısı denir.

Sıralama Bağıntısı

A'da tanımlı bir bağıntının

1. Yansıma
2. Ters-simetri
3. Geçişme

özellikleri varsa bu bağıntıya sıralama bağıntısı denir.

Mutlak Değer

Mutlak Değer

Bir sayının, sayı sayı doğrusunda belirttiği noktanın uzaklığına, bu sayının mutlak değeri denir. 

Sayı doğrusunda 0 ile 4 noktalarının arası 4 birimdir. Aynı şekilde 0 ile -4 noktalarının arası da 4 birimdir. Öyleyse |-4| = |4| diyebiliriz.

Bu yüzden mutlak değerin içi negatif olsa da uzaklık değerleri negatif olamayacağı için dışarıya pozitif olarak çıkar.

Bu durumu şöyle kurallaştırabiliriz. Eğer mutlak değerinin içi pozitifse dışarı aynen çıkar. Eğer mutlak değerin içi negatif ise dışarı işaret değiştirerek çıkar. Bu durumu bir örnekle açıklayalım. 

Örnek: x < 0 < y olmak üzere |x - y| + |y - x| ifadesini bulunuz. 

Çözüm: Mutlak değer 0 (orjin) noktasına uzaklık demekse ve her zaman pozitif olarak dışarı çıkıyorsa o zaman ilk olarak mutlak değerin içinin işaretini bulmamız gerekir.

x - y ifadesinde x negatif y de pozitif olduğuna göre negatif bir sayıdan pozitif bir sayı çıkarıldığında sonucun yine negatif bir sayı olduğunu biliyoruz. Öyleyse x - y ifadesi negatif bir değere sahiptir ve dışarı işaret değiştirerek çıkar. Yani -(x - y) olur. O da y - x değerine eşittir. 

Bulduğumuz ilk sonuç |x - y| = y - x şeklindedir.

 y - x ifadesini incelersek pozitif bir sayıdan negatif bir sayı çıkarıldığında sonucun pozitif olacağını kolaylıkla fark edebiliriz. Pozitif değerli ifadeler de mutlak değerin dışına aynen çıkar. 

Öyleyse bulduğumuz ikinci sonuç |y - x| = y - x olur. 

Bu iki sonucu birleştirirsek (y - x) + (y - x) = 2(y - x) olur. Bu da 2y - 2x ifadesine eşittir.

Mutlak Değerin Özellikleri

1. |x| ≥ 0
2. |x| = |-x|
3. -|x| ≤ x ≤ |x|
4. |x.y| = |x|.|y|

Bu dört özelliği kullanıp yeni özellikler türetebiliriz. En genel olarak bu dört özelliği bilmemiz diğer özellikleri elde etmemiz için yeterli olacaktır.

|x - a| = b ifadesi x'in b'den a birim kadar uzakta olduğunu ifade eder. Bu uzaklığın pozitif yönde veya negatif yönde olması önemli değildir. 

Örnek: A = |x - 3| + |x + 2| ifadesinin en küçük değeri nedir?

Çözüm: Soruda A'nın en küçük değeri isteniyor. Öyleyse x'in -2 ve 3 aralığında bir değer alması gerekmektedir. Çünkü bu aralağın dışına çıkarsa x uzaklık değerlerinin toplamı daha büyük olacaktır. x'e değer verirken de -2 ≤ x ≤ 3 şeklindeki değer aralığından bir değer seçilir. Mesela 0 değerini alırsak 3 +2 = 5 olur. Aynı şekilde 1 alırsak 2 + 3 = 5 olur. Demek ki sayı doğrusunda bu aralıkta bulunan bütün sayılar A'nın en küçük değerini elde etmemizi sağlıyor.

Yani en küçük değer 5 olur.

Köklü Sayılar

Köklü Sayılar

xn = a ise, x = n√a  ifadesinde x sayısına a nın n. dereceden kökü denir.

Köklü Sayıların Özellikleri

1.  n√a  ifadesnin bir reel sayı olabilmesi için x ≥ 0 veya n tek sayı olmalıdır.
2. n√am = am / n dir.
3. a ≥ 0 ve n tek sayı ise n√an = a olur.
4. a ≥ 0 ven çift sayı ise n√an = |a| olur. 
5. n√1  = 1 ve n√0  = 0 dır.
6. k bir doğal sayı ve a > 0 ise n√am = n.k√am.k dır.
7. k > 0 ise, k.n√a = n√akn olur.
8. an√x  + bn√x  - cn√x  = (a + b - c)n√x  dir.
9. n√x .n√y  = n√x . y  dir. 
10. y ≠ 0 ise n√x  / n√y  = n√x / y  dir.
11. (√a  - √b  ).( √a  + √b  ) = a - b dir.
12. a < b ⇒ n√a < n√b dir.

 Örnek:

4√3 - x   + √x + 4 

toplamının reel sayı olabilmesi için x in alabileceği değerlerin en geniş aralığını bulalım. 

Çözüm:

4√3 - x   + √x + 4  ifadesinin bir reel sayı olabilmesi için köklerin içi negatif olmamalıdır.

(3 - x) ve (x + 4) ifadeleri 0 a eşit veya 0 dan büyük olmalıdır.

x sayısı -4 den 3 e kadar değer alabilir.

Buna göre; x, [-4, 3] aralığında olmalıdır.

Örnek:

(25)n = 9

olduğuna göre, (125)n nin pozitif değeri kaçtır?

Çözüm:

25n = (52)n

(52)n = (5n)2 = 9

5n = 3

125n = (5n)3 = 33 = 27