Geometrik Kavramlar ve Doğruda Açılar
Bu konuda geometri dersinde kullanılan temel kavramlarla birlikte doğrusal bir zeminde (düzlemde) açılar konusu işlenecektir. Bu konuların kavranması geometrinin daha sonra gelen konularının anlaşılması için de önemlidir.
Geometrik Kavramlar
Geometri, Latince bir kelime olup yer ölçüsü manasına gelmektedir, insanların, gördükleri tüm eşyayı ölçme ihtiyacından doğmuştur. Tarih boyunca, medeniyetlerin katkılarıyla ölçme teknikleri geliştirilerek bugünkü geometri bilimine ulaşılmıştır.
Geometri tekniklerini iyi öğrenebilmek için, geometri ile ilgili kavramları iyice anlamanız gerekir.
Nokta: Nokta, geometrinin en temel kavramıdır ve tanımsızdır. Eni, boyu ve yüksekliği yoktur. Büyük harflerle adlandırılır. Tanımsız olduğu için noktayı, ince uçlu bir kalemin ucunun kağıda dokundurulduğunda bıraktığı iz olarak düşünebilirsiniz.
Bir kâğıdı, kat yerleri kesişecek biçimde dörde katlayıp açarsanız kat yerlerinin kesişimi, nokta kavramı için iyi bir modeldir.
Doğru: Noktada olduğu gibi, doğrunun da bir tanımı yoktur. Bir kâğıdı ikiye katlayıp açtığımızda elde edilen kat yeri doğruyu modeller. Doğrunun sadece boyu vardır ve her iki yönde sonsuza uzar.
A ve B noktalarından geçen doğru AB olarak gösterilir ve "AB doğrusu" olarak okunur. A ve B noktalarının ikisinden AB doğrusu dışında başka bir doğru da geçmez. Çünkü iki noktadan yalnız bir doğru geçer.
Doğrular bazen küçük harflerle de gösterilebilir. Yani üzerinde bulunan harfler belirtilmeden doğrudan d doğrusu diye adlandırılıbilirler.
Aşağıdaki şekilde verilen ℓ doğrusu A noktasından geçtiği için, "A noktası ℓ doğrusu üzerindedir." denir ve A ∈ ℓ şeklinde gösterilir. B noktası ℓ doğrusu üzerinde olmadığı için, bu durum B ∉ ℓ şeklinde gösterilir.
Noktaların Doğrusallığı
Şekildeki ℓ doğrusu üzerinde verilen A, B, C noktaları aynı doğru üzerinde bulunduğundan "A, B ve C noktaları doğrusaldır." denir. A, B ve D noktaları ya da B, C ve D noktaları aynı doğru üzerinde bulunamayacağı için bu noktalar doğrusal değildir. A, C ve D noktalarının üçünden de geçen bir doğru çizebilir misiniz? Kesinlikle çizemezsiniz. Çizmeye kalktığınızda çizdiğiniz şey bir doğru olmayacaktır.
Düzlem: Düzlem de nokta ve doğru gibi tanımsız bir terimdir. Düzgün bir masanın yüzeyini zihninizde sınırsız olarak büyütünüz. O kadar çok büyütün ki kenarları artık gözükmez olsun. Zihninizde oluşan kalınlıksız yüzey, düzlem için iyi bir modeldir.
Düzlemler paralelkenar ile gösterilir. E, F, K gibi büyük harflerle adlandırılır. Düzlemler de doğru ve noktalar gibi farklı konumlarda bulunabilirler. Karşımızdaki duvar düşey düzlem, yerin zemini yatay düzlemdir. Sınıftaki yazı tahtası da iyi bir düzlem örneğidir.
Düzlemde her şey iki boyutludur. Bir düzleme çizdiğiniz şeklin eni ve boyu olabilir ancak ona üçüncü boyutu veren yüksekliği olmaz. Sınıf tahtasına işaret parmağınızı dik bir şekilde koyarsanız o zaman düzleme yükseklik kazandırmış olursunuz.
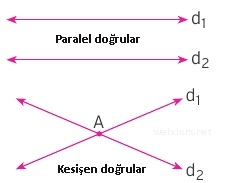
Doğruların Paralelliği
Aynı düzlemde bulunan ve kesişmeyen doğrulara paralel doğrular denir. İki doğru aynı düzlemdeyse ya paralellerdir ya da kesişirler. Paralel iki doğru sonsuza kadar giderler ve hiçbir noktada kesişmezler.
Doğruların Kesişmesi
İki doğru ortak tek bir nokta barındırıyorsa bu doğrular o noktada kesişiyor demektir. Paralel olmayan iki doğru aynı düzlemdelerse mutlaka kesişeceklerdir. Tek bir nokta diye belirtmemizin nedeni ise şudur: Eğer iki doğrunun bütün noktaları aynıysa o zaman üst üste çizilmiş iki doğrudan bahsetmekteyizdir. Bu doğrulara da çakışık doğrular deriz.
Doğru parçası: Bir doğru üzerinde başlangıç ve bitiş noktası belli olan parçaya doğru parçası denir. Doğru parçası köşeli parantezle gösterilir. A noktasından B noktasına giden bir doğru parçasını [AB] doğru parçası diye adlandırırız. Doğru parçasının üzerindeki noktalar doğrusaldır. Doğru parçasının uzunluğu ise mutlak değer sembolüyle gösterilir. [AB] doğru parçasının uzunluğunu |AB| diye gösteririz.
Koordinat Doğrusu
Gerçek sayıların, bir doğrunun noktaları ile birebir eşlenmesi ile oluşturulan sayı doğrusuna koordinat doğrusu, doğrunun üzerinde 0 sayısına karşılık gelen noktaya başlangıç noktası (orijin) denir. Herhangi bir noktaya karşılık gelen gerçek sayıya bu noktanın koordinatı adı verilir.
İki Nokta Arası Uzaklık
Koordinatları A(a) ve B(b) olan iki nokta arasındaki uzaklık d(A, B) olarak ifade edilir ve bu uzunluk d(A, B) = |b - a| eşitliğiyle bulunur.
|x| ifadesi ise, x sayısının sıfıra olan uzaklığını verir. Ayrıca, uzunluğu eşit olan doğru parçalarına eş doğru parçaları denir.
Işın: Bir doğru üzerindeki sabit bir noktadan başlayan yönlü doğru parçasına denir. Doğru parçasından farklı yönlü olmasıdır. Yani bir tarafa doğru sonsuza kadar gider. Bir noktanın bir yere ışınlanması şeklinde akılda tutulabilir. Işın da köşeli parantezle gösterilir. Ancak ışının bir bitiş noktası olmadığı için bir tarafında parantez bulunmaz. Örneğin [AB ışını A noktasından başlayıp B noktasından geçerek sonsuza kadar giden bir noktalar kümesidir.
Aynı yerden başlayan iki ışın bir açıyı oluşturur. Işınlar üst üste çakışık durumdaysa aradaki açı 0 olur.
Başlangıç noktaları ortak olan iki ışının birleşim kümesine açı; açıyı oluşturan ışınların her birine açının kenarları (veya kolları) ve bu iki ışının ortak olan başlangıç noktasına açının köşesi denir.
Şekilde [OA ve [OB ışınları açının kolları, O noktası ise açının köşesidir.
Burada [OA ve [OB ışınlarının oluşturduğu açı, AOB şeklinde gösterilir ve "AOB açısı" diye okunur. Açılar isimlendirilirken açının köşesi ve kenarları üzerindeki noktalar kullanılır. Şekildeki açı AOB açısı, BOA açısı veya sadece O açısı şeklinde isimlendirilir.
Açı Ölçüm Birimleri
Geometride en çok kullanılan açı ölçüm birimi derecedir. Doğruda açılar konusundan başlayarak en karmaşık geometri konusuna kadar derece kavramıyla karşılaşırız. Bir çember 360 dereceyi ifade eder. Bir doğru ise 180 dereceyi. 1 derecenin 60'ta birine 1 dakika (1') denir. 1 dakikanın ise 60'ta birine ise 1 saniye (1'') denir. Dereceden sonra en çok kullanılan açı ölçü birimi ise radyandır. Radyan bir çemberin çevresinin 2π ile orantılı olduğunu bilgisinden kaynaklanır. 2π = 360° şeklinde bir eşitlik kurabiliriz.
Açıortay
Bir açıyı iki eşit parçaya bölen ışına verilen addır. Açıortay sonraki konularda da işimize çok yarayacak bir geometrik kavramdır.
Şekilde [OC ışını AOB açısının açıortayıdır. Yani sağında ve solunda kalan iki açı da eşit derecede ve AOB açısının yarısı kadardır. Birbirine hemen komşu olan açıortayla ya da herhangi bir ışınla ayrılmış açılara ise komşu açılar deriz.
Yukarıdaki şekilde BAC açısı ile CAD açısı birer komşu açıdır.
Ölçülerine Göre Açı Türleri
Açıları sınıflandırırken birden fazla parametre kullanılır. Ancak açının genişliği açı türlerini belirlemek için temel kriterdir. Dar açı, dik açı, geniş açı, doğru açı, tam açı en bilinen açı türleridir. Bu açılar oluşturulurken açı genişlikleri esas alınmıştır.
Ölçüsü 0 ile 90 derece arasında olan açılara dar açı denir.
Ölçüsü 90 derece olan açılara dik açı denir.
Ölçüsü 90 derece ile 180 derece arasında olan açılara geniş açı denir.
Ölçüsü 180 derece olan açıya doğru açı denir. 180 derecelik bir açı bir doğru belirtir.
Ölçüsü 360 derece olan açıya tam açı denir. Tam açı bir çember ölçüsü şeklindedir.
Ters Açı, Tümler Açı, Bütünler Açı
Açıların birbirlerine göre durumları da önemlidir. Ters açı, tümler açı ve bütünler açı açıların birbirlerine göre konumlarından dolayı ortaya çıkmış geometrik kavramlardır.
Ters açıların ölçüsü birbirine eşit olur. Tümler açıların toplamı 90 derecedir. Bütünler açıların toplamı ise 180 derecedir. Buradan şu sonucu çıkarabiliriz. Eğer iki tümler açı komşuysa ikisi birlikte bir dik açı oluşturur. Aynı şekilde bütünler iki açı da bir doğru açı oluşturur.
Tümler ve bütünler açılar ile ilgi çeşitli problemler karşımıza çıkmaktadır. Bu problemleri bu açıların toplamından faydanalarak denklem kurma yoluyla çözeriz.
Paralel İki Doğrunun Bir Kesenle Yaptığı Açılar
Doğruda açılar konusu ile ilgili sorular daha çok bu başlık altında sorulmaktadır. Paralel iki doğruyu başka bir doğru ile kestiğimiz zaman ortaya 8 tane açı çıkar. Bu açılar arasındaki ilişkiler de oldukça önemlidir.
Şekilde k doğrusu paralel olan d1 ve d2 doğrusunu keserek 8 tane açı ortaya çıkarmaktadır. Ortaya çıkan açılar arasında çeşitli eşitlikler vardır.
1=5, 2=6, 3=7, 4=8 (Yöndeş açılar eşittir.)
3=5, 4=6 (İç ters açılar eşittir.)
1=7, 2=8 (Dış ters açılar eşittir.)
1=3, 2=4, 5=7, 6=8 (Ters açılar eşittir.)
Sonuç olarak 1=3=5=7 ve 2=4=6=8 olmak üzere iki farklı büyüklükte açılar çıkar. Bu iki açıların toplamı da 180 derece olduğu için bu açılar bütünler açılardır. Yani 1 ile 2 ya da 1 ile 4 bütünler açılardır diyebiliriz.




















Hiç yorum yok:
Yorum Gönder